Línea de asignación de capital (CAL) y cartera óptima

La Línea de asignación de capital (CAL) es una línea que representa gráficamente el perfil de riesgo y recompensa de los activos, y se puede utilizar para encontrar la cartera óptima. El proceso para construir la CAL para una colección de carteras se describe a continuación.

Rentabilidad y variación esperada de la cartera

Por el bien de la simplicidad, construiremos una cartera con solo dos activos de riesgo.

El rendimiento esperado de la cartera es un promedio ponderado de los rendimientos esperados de sus activos individuales, y se calcula como:

E (Rp) =w ₁ E (R ₁ ) + w ₂ E (R ₂ )

Donde w ₁ , w ₂ son las ponderaciones respectivas de los dos activos, y E (R ₁ ), E (R ₂ ) son los respectivos rendimientos esperados.

Los niveles de varianza se traducen directamente con los niveles de riesgo; mayor varianza significa mayores niveles de riesgo y viceversa. La varianza de una cartera no es solo el promedio ponderado de la varianza de los activos individuales, sino que también depende de la covarianza y correlación de los dos activos. La fórmula para la variación de la cartera se da como:

Var (R _pag ) =w ² ₁ Var (R ₁ ) + w ² ₂ Var (R ₂ ) + 2w ₁ w ₂ Cov (R ₁ , R ₂ )

Donde Cov (R ₁ , R ₂ ) representa la covarianza de los dos rendimientos de los activos. Alternativamente, la fórmula se puede escribir como:

σ ² _pag =w ² ₁ σ ² ₁ + w ² ₂ σ ² ₂ + 2ρ (R ₁ , R ₂ ) w ₁ w ₂ σ ₁ σ ₂ , usando ρ (R ₁ , R ₂ ), la correlación de R ₁ y R ₂ .

La conversión entre correlación y covarianza se da como:ρ (R ₁ , R ₂ ) =Cov (R ₁ , R ₂ ) / σ ₁ σ ₂ .

La varianza del rendimiento de la cartera es mayor cuando la covarianza de los dos activos es positiva, y menos cuando es negativo. Dado que la varianza representa riesgo, el riesgo de la cartera es menor cuando los componentes de sus activos poseen covarianza negativa. La diversificación es una técnica que minimiza el riesgo de la cartera al invertir en activos con covarianza negativa.

En la práctica, no conocemos los rendimientos y las desviaciones estándar de los activos individuales, pero podemos estimar estos valores en función de los valores históricos de estos activos.

La frontera eficiente

Una frontera de cartera es un gráfico que traza todas las carteras posibles con diferentes combinaciones de ponderaciones de activos, con los niveles de desviación estándar de la cartera graficados en el eje xy el rendimiento esperado de la cartera en el eje y.

Para construir una frontera de cartera, primero asignamos valores para E (R ₁ ), E (R ₂ ), stdev (R ₁ ), stdev (R ₂ ), y ρ (R ₁ , R ₂ ). Usando las fórmulas anteriores, luego calculamos el rendimiento esperado de la cartera y la varianza para cada posible combinación de ponderaciones de activos (w ₂ =1-w ₁ ). Este proceso se puede realizar fácilmente en Microsoft Excel, como se muestra en el siguiente ejemplo:

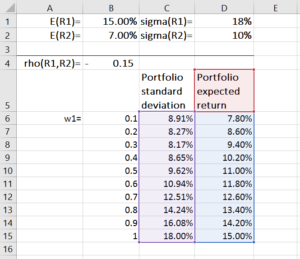
Luego usamos el gráfico de dispersión con líneas suaves para trazar el rendimiento esperado y la desviación estándar de la cartera. El resultado se muestra en el gráfico a continuación, donde cada punto del gráfico representa una cartera construida bajo una combinación de ponderación de activos.

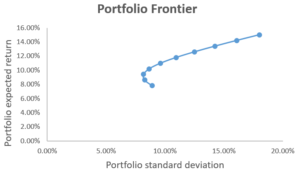
Entonces, ¿cómo sabemos qué carteras son atractivas para los inversores? Para responder a esto, introducimos el concepto de criterio de varianza media , que establece que la Cartera A domina la Cartera B si E (R _A ) ≥ E (R _B ) y σ _A ≤ σ _B (es decir, la cartera A ofrece un rendimiento esperado más alto y un riesgo menor que la cartera B). Si ese es el caso, entonces los inversores preferirían A a B.

Del gráfico, Podemos inferir que las carteras de la parte de pendiente negativa de la frontera de la cartera están dominadas por la parte de pendiente positiva. Como tal, los puntos en la parte de pendiente positiva de la frontera de la cartera representan carteras que los inversores encuentran atractivas, mientras que los puntos en la porción de pendiente negativa representan carteras que son ineficientes.

Según el criterio de varianza media, cualquier inversor seleccionaría de manera óptima una cartera en la parte de pendiente positiva de la frontera de la cartera, que se llama el frontera eficiente , o frontera de varianza mínima . La elección de cualquier cartera en la frontera eficiente depende de las preferencias de riesgo del inversor.

Una cartera por encima de la frontera eficiente es imposible, mientras que una cartera por debajo de la frontera eficiente es ineficiente.

Línea completa de cartera y asignación de capital

Al construir carteras, los inversores a menudo combinan activos de riesgo con activos libres de riesgo (como los bonos del gobierno) para reducir los riesgos. Una cartera completa se define como una combinación de una cartera de activos de riesgo, con retorno R _pag , y el activo libre de riesgo, con retorno R _F .

El rendimiento esperado de una cartera completa se da como:

E (R _C ) =w _pag E (R _pag ) + (1 - w _pag ) R _F

Y la varianza y la desviación estándar del rendimiento completo de la cartera se dan como:

Var (R _C ) =w ² _pag Var (R _pag ), σ (R _C ) =w _pag σ (R _pag ),

donde w _pag es la fracción invertida en la cartera de activos de riesgo.

Mientras que el exceso de rendimiento esperado de una cartera completa se calcula como:

E (R _C ) - R _F ,

si sustituimos E (R _C ) con la fórmula anterior, obtenemos w _pag (E (R _pag ) - R _F ).

La desviación estándar de la cartera completa es σ (R _C ) =w _pag σ (R _pag ), que nos da:

w _pag =σ (R _C ) / σ (R _pag )

Por lo tanto, para cada portafolio completo:

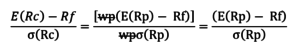
O E (R _C ) =R _F + S _pag σ (R _C ), donde S _pag =

La línea E (R _C ) =R _F + S _pag σ (R _C ) es la línea de asignación de capital (CAL). La pendiente de la línea S _pag , se llama el Relación de Sharpe Relación de Sharpe La relación de Sharpe es una medida del rendimiento ajustado al riesgo, que compara el exceso de rendimiento de una inversión con su desviación estándar de rendimiento. El índice de Sharpe se usa comúnmente para medir el rendimiento de una inversión ajustando su riesgo. o relación recompensa-riesgo. El índice de Sharpe mide el aumento del rendimiento esperado por unidad de desviación estándar adicional.

Portafolio óptimo

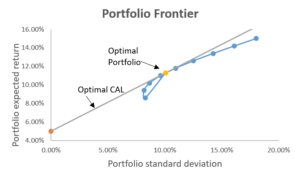
La cartera óptima consta de un activo libre de riesgo y una cartera de activos riesgosa óptima. La cartera de activos de riesgo óptima se encuentra en el punto donde la CAL es tangente a la frontera eficiente. Esta cartera es óptima porque la pendiente de CAL es la más alta, lo que significa que logramos la mayor rentabilidad por unidad adicional de riesgo. El siguiente gráfico ilustra esto:

Las ponderaciones de la cartera tangente se calculan de la siguiente manera:

Resumen de la línea de asignación de capital

Los inversores utilizan tanto la frontera eficiente como la CAL para lograr diferentes combinaciones de riesgo y rendimiento en función de lo que desean. La cartera de riesgo óptima se encuentra en el punto donde la CAL es tangente a la frontera eficiente. Esta combinación de ponderaciones de activos ofrece la mejor relación riesgo-recompensa, ya que tiene la pendiente más alta para CAL.

Descarga la plantilla gratuita

Ingrese su nombre y correo electrónico en el formulario a continuación y descargue la plantilla gratuita ahora.

Recursos adicionales

Gracias por leer la guía de CFI sobre la línea de asignación de capital. Para avanzar en su carrera como Analista de Valoración y Modelado Financiero Conviértase en Analista Certificado de Valoración y Modelado Financiero (FMVA) ® La certificación Analista de Valoración y Modelado Financiero (FMVA) ® de CFI le ayudará a ganar la confianza que necesita en su carrera financiera. ¡Inscríbete hoy! estos recursos adicionales serán útiles:

• Perfil profesional de gestión de carteras Perfil profesional de gestión de carteras La gestión de carteras consiste en gestionar inversiones y activos para los clientes, que incluyen fondos de pensiones, bancos, los fondos de cobertura, oficinas familiares. El administrador de la cartera es responsable de mantener la combinación de activos y la estrategia de inversión adecuadas que se adapten a las necesidades del cliente. Salario, habilidades,
• Prima de riesgo de mercado Prima de riesgo de mercado La prima de riesgo de mercado es el rendimiento adicional que un inversor espera de tener una cartera de mercado riesgosa en lugar de activos libres de riesgo.
• Definición del ratio de Sharpe Ratio de Sharpe El ratio de Sharpe es una medida del rendimiento ajustado al riesgo, que compara el exceso de rendimiento de una inversión con su desviación estándar de rendimiento. El índice de Sharpe se usa comúnmente para medir el rendimiento de una inversión ajustando su riesgo.
• Calculadora de relación de Sharpe Calculadora de relación de Sharpe La calculadora de relación de Sharpe le permite medir el rendimiento ajustado al riesgo de una inversión. Descargue la plantilla de Excel de CFI y la calculadora de índices de Sharpe. Relación de Sharpe =(Rx - Rf) / StdDev Rx. Donde:Rx =Rendimiento esperado de la cartera, Rf =tasa de rendimiento libre de riesgo, StdDev Rx =Desviación estándar del rendimiento / volatilidad de la cartera