Definición de relación lineal

¿Qué es una relación lineal?

Una relación lineal (o asociación lineal) es un término estadístico que se utiliza para describir una relación lineal entre dos variables. Las relaciones lineales se pueden expresar en un formato gráfico donde la variable y la constante están conectadas a través de una línea recta o en un formato matemático donde la variable independiente se multiplica por el coeficiente de pendiente, sumado por una constante, que determina la variable dependiente.

Una relación lineal puede contrastarse con una relación polinomial o no lineal (curva).

Conclusiones clave

• Una relación lineal (o asociación lineal) es un término estadístico que se utiliza para describir una relación lineal entre dos variables.
• Las relaciones lineales se pueden expresar en formato gráfico o como una ecuación matemática de la forma y =mx + b.
• Las relaciones lineales son bastante comunes en la vida diaria.

La ecuación lineal es:

Matemáticamente, una relación lineal es aquella que satisface la ecuación:

Y =mx + b donde:m =pendienteb =intersección con el eje y

En esta ecuación, “X” e “y” son dos variables que están relacionadas por los parámetros “m” y “b”. Gráficamente, y =mx + b se traza en el plano x-y como una línea con pendiente "m" e intersección con el eje y "b". La intersección con el eje y "b" es simplemente el valor de "y" cuando x =0. La pendiente "m" se calcula a partir de dos puntos individuales cualesquiera (x ₁ , y ₁ ) y (x ₂ , y ₂ ) como:

$\mathrm{metro}=\frac{(y_2-y_1)}{(X_2-X_1)}m\; =\backslash \; frac\; \{(y\_2\; -\; y\_1)\}\; \{(x\_2\; -\; x\_1)\}$ m =(x2 −x1) (y2 −y1)

Relación lineal

¿Qué te dice una relación lineal?

Hay tres conjuntos de criterios necesarios que una ecuación debe cumplir para calificar como lineal:una ecuación que expresa una relación lineal no puede constar de más de dos variables, todas las variables en una ecuación deben ser elevadas a la primera potencia, y la ecuación debe representar una línea recta.

Una relación lineal comúnmente utilizada es una correlación, que describe qué tan cerca de la moda lineal cambia una variable en relación con los cambios en otra variable.

En econometría, La regresión lineal es un método de uso frecuente para generar relaciones lineales para explicar varios fenómenos. Se usa comúnmente para extrapolar eventos del pasado para hacer pronósticos para el futuro. No todas las relaciones son lineales, sin embargo. Algunos datos describen relaciones que son curvas (como relaciones polinomiales) mientras que otros datos no se pueden parametrizar.

Funciones lineales

Matemáticamente similar a una relación lineal es el concepto de función lineal. En una variable, una función lineal se puede escribir de la siguiente manera:

F (x) =mx + b donde:m =pendienteb =intersección con el eje y

Esto es idéntico a la fórmula dada para una relación lineal excepto que el símbolo f (x) se usa en lugar de y. Esta sustitución se hace para resaltar el significado de que x se asigna af (x), mientras que el uso de y simplemente indica que xey son dos cantidades, relacionado por A y B.

En el estudio del álgebra lineal, las propiedades de las funciones lineales se estudian extensamente y se hacen rigurosas. Dado un escalar C y dos vectores A y B de R ^norte , la definición más general de una función lineal establece que:$C\times F(A+B)=C\times F\left(A\right)+C\times F\left(B\right)c\; \backslash \; times\; f\; (A\; +\; B)\; =c\; \backslash \; times\; f\; (A)\; +\; c\; \backslash \; times\; f\; (B)$ c × f (A + B) =c × f (A) + c × f (B)

Ejemplos de relaciones lineales

Ejemplo 1

Las relaciones lineales son bastante comunes en la vida diaria. Tomemos el concepto de velocidad, por ejemplo. La fórmula que usamos para calcular la velocidad es la siguiente:la tasa de velocidad es la distancia recorrida en el tiempo. Si alguien en una minivan blanca Chrysler Town and Country 2007 viaja entre Sacramento y Marysville en California, un tramo de 41,3 millas en la autopista 99, y el viaje completo termina en 40 minutos, habrá viajado a menos de 60 mph.

Si bien hay más de dos variables en esta ecuación, sigue siendo una ecuación lineal porque una de las variables siempre será una constante (distancia).

Ejemplo 2

También se puede encontrar una relación lineal en la ecuación distancia =tasa x tiempo. Como la distancia es un número positivo (en la mayoría de los casos), esta relación lineal se expresaría en el cuadrante superior derecho de un gráfico con ejes X e Y.

Si una bicicleta hecha para dos viajaba a una velocidad de 30 millas por hora durante 20 horas, el ciclista terminará viajando 600 millas. Representado gráficamente con la distancia en el eje Y y el tiempo en el eje X, una línea que rastrea la distancia durante esas 20 horas viajaría directamente desde la convergencia de los ejes X e Y.

Ejemplo 3

Para convertir Celsius a Fahrenheit, o Fahrenheit a Celsius, usarías las ecuaciones siguientes. Estas ecuaciones expresan una relación lineal en una gráfica:

$°C=\frac{5}{9}(°F-32)\backslash \; grado\; C\; =\backslash \; frac\; \{5\}\; \{9\}\; (\backslash \; grado\; F\; -\; 32)$ ° C =95 (° F − 32)

$°F=\frac{9}{5}°C+32\backslash \; grado\; F\; =\backslash \; frac\; \{9\}\; \{5\}\; \backslash \; grado\; C\; +\; 32$ ° F =59 ° C + 32

Ejemplo 4

Suponga que la variable independiente es el tamaño de una casa (medido en pies cuadrados) que determina el precio de mercado de una casa (la variable dependiente) cuando se multiplica por el coeficiente de pendiente de 207,65 y luego se suma al término constante $ 10 , 500. Si los pies cuadrados de una casa son 1, 250 entonces el valor de mercado de la casa es (1, 250 x 207,65) + $ 10, 500 =$ 270, 062.50. Gráficamente, y matemáticamente aparece de la siguiente manera:

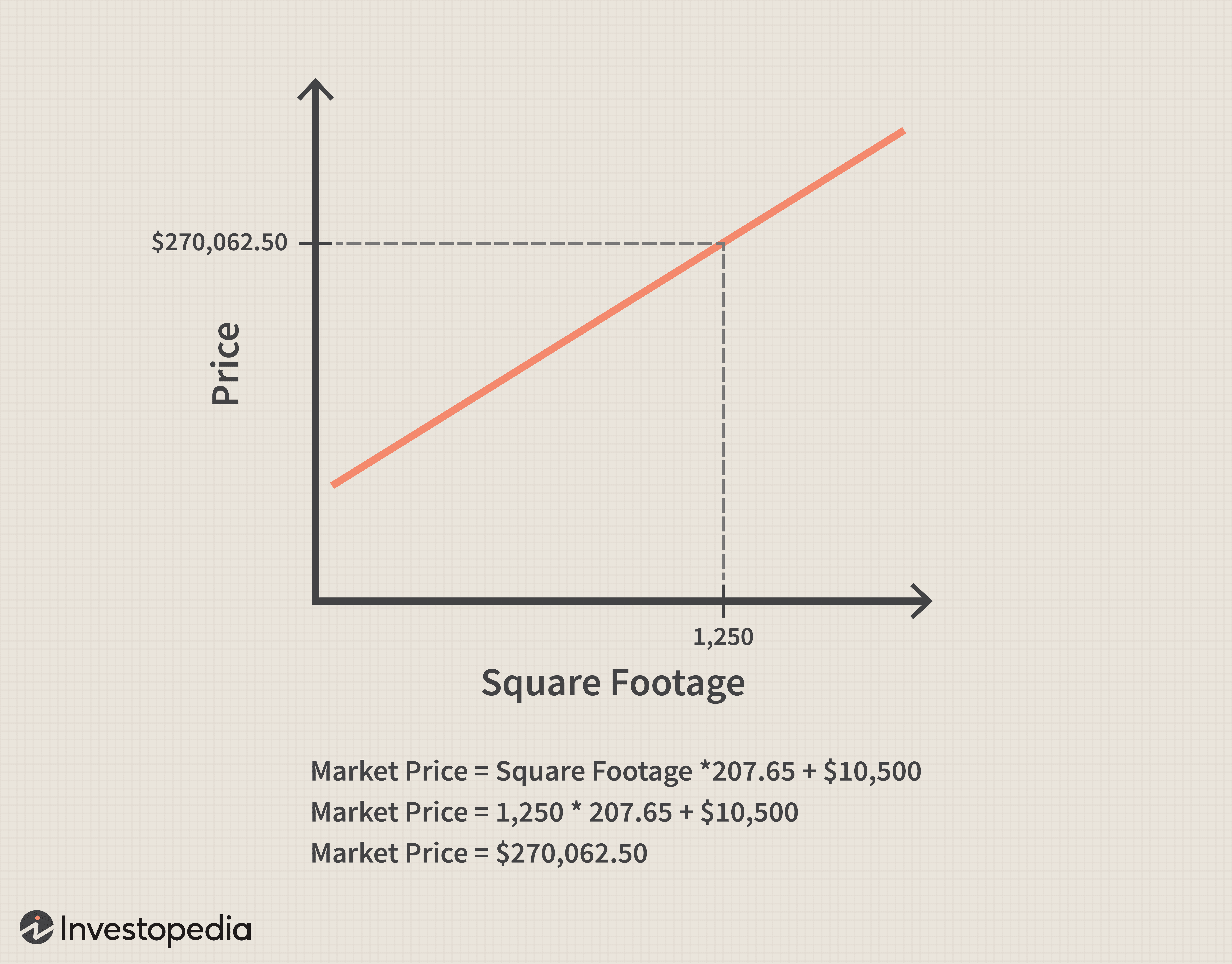
En este ejemplo, a medida que aumenta el tamaño de la casa, el valor de mercado de la casa aumenta de forma lineal.

Algunas relaciones lineales entre dos objetos pueden denominarse "relación proporcional". Esta relación aparece como

Y =k × X donde:k =constante Y, X =cantidades proporcionales

Al analizar datos de comportamiento, Rara vez existe una relación lineal perfecta entre las variables. Sin embargo, Las líneas de tendencia se pueden encontrar en los datos que forman una versión aproximada de una relación lineal. Por ejemplo, podría considerar las ventas diarias de helado y la temperatura máxima diaria como las dos variables en juego en un gráfico y encontrar una relación lineal cruda entre las dos.