Cómo interpolar tasas de interés
 La interpolación lineal estima valores entre puntos de datos.
La interpolación lineal estima valores entre puntos de datos. La interpolación es un proceso matemático para estimar el valor de una variable dependiente en función de los valores de las variables dependientes circundantes conocidas, donde la variable dependiente es una función de una variable independiente. Se utiliza para determinar las tasas de interés para períodos de tiempo que no se publican o no están disponibles de otra manera. En este caso, la tasa de interés es la variable dependiente, y el tiempo es la variable independiente. Para interpolar una tasa de interés, necesitará la tasa de interés de un período de tiempo más corto y un período de tiempo más largo.
Paso 1
Reste la tasa de interés de un período de tiempo más corto que el período de tiempo de la tasa de interés deseada de la tasa de interés de un período de tiempo más largo que el período de tiempo de la tasa de interés deseada. Por ejemplo, si está interpolando una tasa de interés a 45 días, y la tasa de interés a 30 días es 4.2242 por ciento y la tasa de interés a 60 días es 4.4855 por ciento, la diferencia entre las dos tasas de interés conocidas es 0.2613 por ciento.
Paso 2
Divida el resultado del Paso 1 por la diferencia entre la duración de los dos períodos de tiempo. Por ejemplo, la diferencia entre el período de 60 días y el período de 30 días es de 30 días. Dividir 0.2613 por ciento por 30 días y el resultado es 0.00871 por ciento.
Paso 3
Multiplique el resultado del Paso 2 por la diferencia entre el período de tiempo para la tasa de interés deseada y el período de tiempo para la tasa de interés con el período de tiempo más corto. Por ejemplo, la tasa de interés deseada es de 45 días, y la tasa de interés más corta conocida es la tasa a 30 días. La diferencia entre 45 días y 30 días es de 15 días. 15 multiplicado por 0,00871 por ciento es igual a 0,13065 por ciento.
Paso 4
Agregue el resultado del Paso 3 a la tasa de interés para el período de tiempo más corto conocido. Por ejemplo, la tasa de interés del período de 30 días es 4.2242 por ciento. La suma de 4.2242 por ciento y 0.13065 por ciento es 4.35485 por ciento. Ésta es la estimación de interpolación para la tasa de interés a 45 días.
Propina
Para asegurarse de que está siguiendo correctamente la ecuación, puede ser útil dibujar un gráfico. El gráfico debe tener un eje que represente las tasas de interés, con el otro eje representando la cantidad de tiempo. Dibuje una línea recta a través de los dos puntos que representan las tasas de interés conocidas. Si la tasa de interés que interpola queda fuera de esta línea, sabrá que cometió un error en el camino.
Advertencia
La interpolación lineal es una estimación de la tasa de interés de un período de tiempo específico, y supone que la tasa de interés cambia de forma lineal entre cada día. En realidad, las tasas de interés pueden seguir una "curva de rendimiento" en lugar de una línea recta. La estimación será más precisa cuanto más corto sea el período de tiempo entre las tasas de interés conocidas de las que está interpolando.
Cosas que necesitará
-
Calculadora
-
Lápiz
-
Papel
Artículos Destacados
- Cómo convertir APR a una tasa de interés diaria
- Cómo calcular las tasas de interés diarias
- Cómo calcular un factor de tasa de interés
- Cómo calcular el interés
- ¿Cómo se calcula el interés acumulado?
- Cómo calcular la tasa de interés implícita
- ¿Cómo afectan las tasas de interés al mercado de valores?
- Cómo afectan las tasas de interés a los fondos mutuos
- ¿Cómo se fijan las tasas de interés?
-
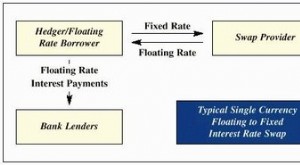 Cómo valorar un swap de tipos de interés
Cómo valorar un swap de tipos de interés Los swaps de tipos de interés equivalen a intercambiar flujos de efectivo, con un flujo basado en pagos variables y el otro en pagos fijos. Para entender si un intercambio es un buen negocio, los inve...
-
 ¿Cómo afectan las tasas de interés a la economía?
¿Cómo afectan las tasas de interés a la economía? Los niveles de las tasas de interés pueden determinar el estado de la economía de EE. UU. Las tasas de interés son una variable económica que afecta a todos los segmentos de la economía. Los consumid...