Definición del teorema de Bayes
¿Qué es el teorema de Bayes?
Teorema de Bayes, nombrado en honor al matemático británico del siglo XVIII Thomas Bayes, es una fórmula matemática para determinar la probabilidad condicional. La probabilidad condicional es la probabilidad de que ocurra un resultado, basado en un resultado previo que ocurrió. El teorema de Bayes proporciona una forma de revisar las predicciones o teorías existentes (actualizar las probabilidades) dada la evidencia nueva o adicional. En finanzas, El teorema de Bayes se puede utilizar para calificar el riesgo de prestar dinero a posibles prestatarios.
El teorema de Bayes también se llama Regla de Bayes o Ley de Bayes y es la base del campo de la estadística Bayesiana.
Conclusiones clave
- El teorema de Bayes le permite actualizar las probabilidades predichas de un evento incorporando nueva información.
- El teorema de Bayes recibió su nombre del matemático del siglo XVIII Thomas Bayes.
- A menudo se emplea en finanzas para actualizar la evaluación de riesgos.
Comprensión del teorema de Bayes
Las aplicaciones del teorema están muy extendidas y no se limitan al ámbito financiero. Como ejemplo, El teorema de Bayes se puede utilizar para determinar la precisión de los resultados de las pruebas médicas teniendo en cuenta la probabilidad de que una persona determinada tenga una enfermedad y la precisión general de la prueba. El teorema de Bayes se basa en incorporar distribuciones de probabilidad previas para generar probabilidades posteriores. Probabilidad previa, en inferencia estadística bayesiana, es la probabilidad de que ocurra un evento antes de que se recopilen nuevos datos. Ésta es la mejor evaluación racional de la probabilidad de un resultado basada en el conocimiento actual antes de realizar un experimento. La probabilidad posterior es la probabilidad revisada de que ocurra un evento después de considerar nueva información. La probabilidad posterior se calcula actualizando la probabilidad anterior mediante el teorema de Bayes. En términos estadísticos, la probabilidad posterior es la probabilidad de que ocurra el evento A dado que el evento B ha ocurrido.
El teorema de Bayes, por lo tanto, da la probabilidad de un evento basado en nueva información, es decir, o puede estar relacionado, a ese evento. La fórmula también se puede utilizar para ver cómo la probabilidad de que ocurra un evento se ve afectada por información nueva hipotética, suponiendo que la nueva información resulte ser cierta. Por ejemplo, digamos que se extrae una sola carta de una baraja completa de 52 cartas. La probabilidad de que la carta sea un rey es cuatro dividida por 52, que equivale a 1/13 o aproximadamente 7,69%. Recuerda que hay cuatro reyes en la baraja. Ahora, supongamos que se revela que la carta seleccionada es una figura. La probabilidad de que la carta seleccionada sea un rey, dado que es una figura, es cuatro dividido por 12, o aproximadamente el 33,3%, ya que hay 12 figuras en una baraja.
Fórmula para el teorema de Bayes
P (A∣B) =P (B) P (A⋂B) =P (B) P (A) ⋅P (B∣A) donde:P (A) =La probabilidad de que ocurra A P (B ) =La probabilidad de que ocurra B P (A∣B) =La probabilidad de que A dado BP (B∣A) =La probabilidad de que B dado AP (A⋂B)) =La probabilidad de que ocurran A y B
Ejemplos del teorema de Bayes
A continuación se muestran dos ejemplos del teorema de Bayes en el que el primer ejemplo muestra cómo se puede derivar la fórmula en un ejemplo de inversión en acciones utilizando Amazon.com Inc. (AMZN). El segundo ejemplo aplica el teorema de Bayes a las pruebas de drogas farmacéuticas.
Derivando la fórmula del teorema de Bayes
El teorema de Bayes se deriva simplemente de los axiomas de probabilidad condicional. La probabilidad condicional es la probabilidad de un evento dado que ocurrió otro evento. Por ejemplo, una simple pregunta de probabilidad puede plantear:"¿Cuál es la probabilidad de que caiga el precio de las acciones de Amazon.com?" La probabilidad condicional lleva esta pregunta un paso más allá al preguntar:"¿Cuál es la probabilidad de que el precio de las acciones de AMZN caiga? Dado que el índice Dow Jones Industrial Average (DJIA) cayó antes? "
La probabilidad condicional de A dado que B ha sucedido se puede expresar como:
Si A es:"el precio AMZN cae", entonces P (AMZN) es la probabilidad de que AMZN caiga; y B es:"DJIA ya está inactivo, "y P (DJIA) es la probabilidad de que el DJIA caiga; entonces la expresión de probabilidad condicional se lee como" la probabilidad de que AMZN caiga dada una caída del DJIA es igual a la probabilidad de que el precio de AMZN baje y el DJIA baje sobre la probabilidad de una disminución en el índice DJIA.
P (AMZN | DJIA) =P (AMZN y DJIA) / P (DJIA)
P (AMZN y DJIA) es la probabilidad de ambos Ocurren A y B. Esto también es lo mismo que la probabilidad de que ocurra A multiplicada por la probabilidad de que ocurra B dado que ocurre A, expresado como P (AMZN) x P (DJIA | AMZN). El hecho de que estas dos expresiones sean iguales conduce al teorema de Bayes, que está escrito como:
si, P (AMZN y DJIA) =P (AMZN) x P (DJIA | AMZN) =P (DJIA) x P (AMZN | DJIA)
luego, P (AMZN | DJIA) =[P (AMZN) x P (DJIA | AMZN)] / P (DJIA).
Donde P (AMZN) y P (DJIA) son las probabilidades de que Amazon y el Dow Jones caigan, sin tener en cuenta el uno al otro.
La fórmula explica la relación entre la probabilidad de la hipótesis antes de ver la evidencia de que P (AMZN), y la probabilidad de la hipótesis después de obtener la evidencia P (AMZN | DJIA), dada una hipótesis para Amazon dada la evidencia en el Dow.
Ejemplo numérico del teorema de Bayes
Como ejemplo numérico, imagina que hay una prueba de drogas con un 98% de precisión, lo que significa que el 98% de las veces muestra un resultado positivo verdadero para alguien que usa la droga y el 98% de las veces muestra un resultado negativo real para los no consumidores de la droga. Próximo, suponga que el 0,5% de las personas consumen la droga. Si una persona seleccionada al azar da positivo por el medicamento, Se puede hacer el siguiente cálculo para ver si la probabilidad de que la persona sea realmente un usuario de la droga.
(0,98 x 0,005) / [(0,98 x 0,005) + ((1 - 0,98) x (1 - 0,005))] =0,0049 / (0,0049 + 0,0199) =19,76%
El teorema de Bayes muestra que incluso si una persona dio positivo en este escenario, en realidad, es mucho más probable que la persona no sea un usuario de la droga.
Finanzas
- Definición de asunción de deuda
- Definición de un co-solicitante
- Definición de media geométrica
- Definición de valoración
- Definición y explicación de la garantía
- Una definición de los tiempos de interés devengados
- Liquidez - Definición y ratios
- Definición y explicación del desembolso
- Fiduciario - Definición y Responsabilidad
-
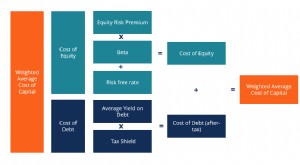 Definición de WACC
Definición de WACC El costo de capital promedio ponderado (WACC) de una empresa representa su costo de capital combinado Costo de capital El costo de capital es la tasa mínima de rendimiento que una empresa debe obtener...
-
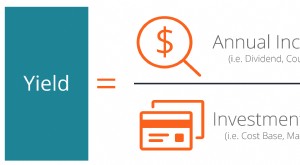 ¿Qué es el rendimiento (definición)?
¿Qué es el rendimiento (definición)? El rendimiento se define como un rendimiento de la inversión solo en función de los ingresos (excluye las ganancias de capital El rendimiento de las ganancias de capital El rendimiento de las ganancia...